一、数据集的下载和处理

下载数据

直接调用官方库

1 2	train_dataset = datasets.MNIST(root='./data', train=True, download=True) test_dataset = datasets.MNIST(root='./data', train=False)

数据处理与分割

将图像数据从二维数组展平为一维数组，方便MLP处理，并将数据除以255以归一化；官方以为我们划分好了训练集和测试集，我们还需从训练集划分10000条数据（与测试集同种规模）到验证集，代码如下：

# 将数据转换为适合训练的格式
img_train = train_dataset.data.view(-1, 28*28).float() / 255.0
label_train = train_dataset.targets
img_test = test_dataset.data.view(-1, 28*28).float() / 255.0
label_test = test_dataset.targets

# 将训练集的后 10,000 条数据作为验证集
img_val = img_train[-10000:]
label_val = label_train[-10000:]
img_train = img_train[:-10000]
label_train = label_train[:-10000]

当前数据集是torch形式，因为我们要用numpy建立神经网络，应该将数据集转化为numpy数组：

img_train_np = img_train.numpy()
label_train_np = label_train.numpy()
img_val_np = img_val.numpy()
label_val_np = label_val.numpy()
img_test_np = img_test.numpy()
label_test_np = label_test.numpy()

数据集加载器

模仿torch的DataLoader，我们也需要一个数据集加载器，以实现下面两种功能

将每次训练所需的batch_size数据进行封装，制成一个迭代器。
在每次epoch开始时，将训练集数据随机打乱，使训练更充分，防止过拟合。

class NumpyDataLoader:
    def __init__(self, dataset, labels, batch_size=64, shuffle=True):
        self.dataset = dataset
        self.labels = labels
        self.batch_size = batch_size
        self.shuffle = shuffle
        self.indices = np.arange(len(dataset))
        self.current_index = 0

        if self.shuffle:
            np.random.shuffle(self.indices)

    def __iter__(self):
        self.current_index = 0
        if self.shuffle:
            np.random.shuffle(self.indices)
        return self

    def __next__(self):
        if self.current_index >= len(self.dataset):
            raise StopIteration

        batch_indices = self.indices[self.current_index:self.current_index + self.batch_size]
        batch_data = self.dataset[batch_indices]
        batch_labels = self.labels[batch_indices]
        self.current_index += self.batch_size

        return batch_data, batch_labels

    def __len__(self):
        return int(np.ceil(len(self.dataset) / self.batch_size))

二、全连接层

全连接层->向前传播

数学模型

$\boldsymbol{y}=\boldsymbol{xW}+\boldsymbol{b}$

其中$\boldsymbol{y}$是输出，$\boldsymbol{x}$是输入，$\boldsymbol{W}$ 是权重矩阵，$\boldsymbol{b}$ 是偏置向量。

代码

1
2
3

def forward(self, x):
    self.x = x
    return np.dot(x, self.W) + self.b

全连接层->反向传播

数学推导

用指标运算重写全连接层的数学模型（采用爱因斯坦求和约定，后续公式也均采用此约定）。

$\boldsymbol{y}_j=\boldsymbol{x}_{i}\boldsymbol{W}_{ij}+\boldsymbol{b}_j$

将$\boldsymbol{y}_j$对每个变量分别求偏导，得到：

$\left\{ \begin{aligned} \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{W}_{ij}} &= \boldsymbol{x}_i, \\ \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{b}_j} &= 1,\\ \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{x}_i} &= \boldsymbol{W}_{ij}. \end{aligned} \right.$

由链式法则，交叉熵损失$\boldsymbol{C}$对$\boldsymbol{y}$的偏导应由后一层网络反向传播求出。在这一层中，我们应在$\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}}$基础上实现$\boldsymbol{C}$对网络参数的偏导，以及将反向传播到下一层中的$\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{x}}$.

$\begin{aligned} \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{W}_{ij}} &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_j} \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{W}_{ij}} \\ &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_j} \boldsymbol{x}_i \\ &= \left( \boldsymbol{x}^T \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}} \right)_{ij} \\ \\ \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{b}_j} &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_i} \frac{\partial \boldsymbol{y}_i}{\partial \boldsymbol{b}_j} \\ &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_i} \delta_{ij} \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{b}_j} \\ &= \left( \mathbf{1} \, \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}} \right)_j \\ \\ \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{x}_i} &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_j} \frac{\partial \boldsymbol{y}_j}{\partial \boldsymbol{x}_i} \\ &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_j} \boldsymbol{W}_{ij} \\ &= \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}_j} \left( \boldsymbol{W} \right)_{ji}^{T} \\ &= \left( \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}} \boldsymbol{W}^T \right)_i \end{aligned}$

在反向传播过程中，$\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{y}}$实际是一个$b\times n$形状的矩阵，$b$为batch_size，$n$为该层网络的输出维度，左乘矩阵同时会对batch_size这一维度求和，用于更新网络的参数，右乘矩阵则会保留bitch_size这一维度，用于反向传播到下一层。

代码

def backward(self, top_grad):
    self.dW = np.dot(self.x.T, top_grad)
    self.db = np.sum(top_grad, axis=0)
    bottom_grad = np.dot(top_grad, self.W.T)
    return bottom_grad

全连接层->参数初始化

数学模型

模仿torch 使用 Kaiming (He) 均匀初始化的参数范围

代码

def __init__(self, input_size, out_size):
    # 模仿torch 使用 Kaiming (He) 均匀初始化的参数范围
    limit_weight = np.sqrt(6 / input_size)
    self.W = np.random.uniform(-limit_weight, limit_weight, (out_size, input_size))
    limit_bias = 1 / np.sqrt(input_size)
    self.b = np.random.uniform(-limit_bias, limit_bias, (1, out_size))

    self.x = None
    self.db = None
    self.dW = None

全连接层->参数更新

数学模型

在所有网络完成反向传播后，对全连接层进行参数更新，采用mini-batch SGD，每一次迭代按照一定的学习率沿梯度的反方向更新参数，直至收敛。

$\boldsymbol{W}\leftarrow\boldsymbol{W}-\eta\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{W}}\\ \boldsymbol{b} \leftarrow \boldsymbol{b} - \eta \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{b}}$

代码

1
2
3

def update_params(self, lr=0.01):
    self.W -= lr * self.dW
    self.b -= lr * self.db

三、ReLU激活层

ReLU层->前向传播

数学模型

$y=\max\left\{0,x\right\}$

代码

1
2
3

def forward(self, x):
    self.x = x
    return np.maximum(0, x)

ReLU层->反向传播

数学推导

$\begin{aligned}\mathrm{ReLU}^{\prime}\left(x\right) & =\left\{\begin{array}{ll}0,x<0\\ 1,x\geqslant0\end{array}\right.\\ & \\ \ \frac{\partial\boldsymbol{C}}{\partial\boldsymbol{x}_i}=\frac{\partial\boldsymbol{C}}{\partial\boldsymbol{y}_i}\mathrm{ReLU}^{\prime}\left(\boldsymbol{x}_{i}\right) & =\left\{\begin{array}{ll}0, & \boldsymbol{x}_{i}<0\\ \frac{\partial\boldsymbol{C}}{\partial\boldsymbol{y}_i}, & \boldsymbol{x}_{i}\geqslant0\end{array}\right.\end{aligned}$

代码

1 2	def backward(self, top_grad): return (self.x > 0) * top_grad

四、Softmax-Loss层

Softmax层->前向传播

数学模型

$\hat{\boldsymbol{y}_i}=\frac{\exp (\boldsymbol{x}_i)}{\sum_{j} \exp (\boldsymbol{x}_j)}$

实际使用中，为了避免指数发散，我们可以对$\boldsymbol{x}$中的每个元素减去最大值。

$\hat{\boldsymbol{y}_i}=\frac{\exp [\boldsymbol{x}_i-\max(\boldsymbol{x})]}{\sum_{j} \exp [\boldsymbol{x}_j-\max(\boldsymbol{x})]}$

代码

def forward(self, x):
        exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
        y_pred = exp_x / np.sum(exp_x, axis=1, keepdims=True)
        self.x = x
        self.y_pred = y_pred
        return y_pred

Loss层->前向传播

数学模型

$C=-\sum_i\boldsymbol{y}_i\ln\boldsymbol{\hat{y}}_i$ $L=\frac{1}{N}\sum_{n=1}^{N} C^{n}$

各变量含义如下：

$\boldsymbol{y}_i$：真实标签的one-hot编码向量。
$\boldsymbol{\hat{y}}_i$：预测的概率分布向量。
$C$：单个样本的交叉熵损失。
$L$：一个batch的平均损失。

(13) 式在单分类任务中可化简为

$C=-\ln\boldsymbol{\hat{y}}_r$

其中，$\boldsymbol{\hat{y}}_r$代表预测为正确类别r的归一化概率。

代码

def forward(self, x):
    exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
    y_pred = exp_x / np.sum(exp_x, axis=1, keepdims=True)
    self.x = x
    self.y_pred = y_pred
    return y_pred
def get_loss(self, labels):
    batch_size = len(labels)
    self.one_hot_labels = np.zeros_like(self.y_pred)
    self.one_hot_labels[np.arange(batch_size), labels] = 1
    loss = -np.sum(self.one_hot_labels * np.log(self.y_pred)) / batch_size
    return loss

Softmax-Loss层->反向传播

数学推导

之所以将Softmax层和Loss层合二为一，是因为两层的反向传播的结果比较简单，为：

$\frac{\partial L}{\partial \boldsymbol{x}}=\frac{1}{N}(\hat{\boldsymbol{y}}-\boldsymbol{y})$

接下来是推导

由$L=\sum_{n=1}^{N} C^{n}$易得

$\frac{\partial L}{\partial \boldsymbol{x}_i}=\frac{1}{N}\sum_{n=1}^{N} \frac{\partial C^n}{\partial \boldsymbol{x}_i}$

对于$C=-\ln\boldsymbol{\hat{y}}_r$，链式求导得（同样使用爱因斯坦求和约定）

$\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{x}_i}=-\frac{1}{\boldsymbol{\hat{y}}_r}\frac{\partial \boldsymbol{\hat{y}}_r}{\partial \boldsymbol{x}_i}$

对于$\frac{\partial \boldsymbol{\hat{y}}_r}{\partial \boldsymbol{x}_i}$，需要分类讨论

当$i=r$时，

$\begin{aligned} \frac{\partial \boldsymbol{\hat{y}}_r}{\partial \boldsymbol{x}_r} &= \frac{1}{\partial \boldsymbol{x}_r} \frac{\exp \left( \boldsymbol{x}_r \right)}{\sum_j{\exp}\left( \boldsymbol{x}_j \right)} \\ &= \frac{\exp \left( \boldsymbol{x}_r \right) \sum_j{\exp}\left( \boldsymbol{x}_j \right) - \exp \left( \boldsymbol{x}_r \right) \exp \left( \boldsymbol{x}_r \right)}{\left( \sum_j{\exp}\left( \boldsymbol{x}_j \right) \right)^2} \\ &= \boldsymbol{\hat{y}}_r - \boldsymbol{\hat{y}}_r^2 \end{aligned}$

当$i\ne r$时，

$\begin{aligned} \frac{\partial \boldsymbol{\hat{y}}_r}{\partial \boldsymbol{x}_i} &= \frac{1}{\partial \boldsymbol{x}_i} \frac{\exp \left( \boldsymbol{x}_r \right)}{\sum_j{\exp}\left( \boldsymbol{x}_j \right)} \\ &= -\frac{\exp \left( \boldsymbol{x}_i \right) \exp \left( \boldsymbol{x}_r \right)}{\left( \sum_j{\exp}\left( \boldsymbol{x}_j \right) \right)^2} \\ &= -\boldsymbol{\hat{y}}_i \boldsymbol{\hat{y}}_r \end{aligned}$

综上所述，

$\begin{aligned} \frac{\partial \boldsymbol{C}}{\partial \boldsymbol{x}_i} &= \begin{cases} \boldsymbol{\hat{y}}_i - 1, & i = r \\ \boldsymbol{\hat{y}}_i, & i \ne r \\ \end{cases} \\ &= \boldsymbol{\hat{y}}_i - \delta_{ir} \end{aligned}$

向量形式为

$\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{x}} =\boldsymbol{\hat{y}}-\boldsymbol{y}$

由(14)式即得证

$\frac{\partial L}{\partial \boldsymbol{x}}=\frac{1}{N}(\hat{\boldsymbol{y}}-\boldsymbol{y})$

代码

def backward(self):
        batch_size = len(self.one_hot_labels)
        bottom_grad = (self.y_pred - self.one_hot_labels) / batch_size
        return bottom_grad

五、搭建全连接神经网络

模型

我们要搭建只有⼀层hidden layer的全连接神经网络，即搭建三层全连接层，再加上最后的Softmax-Loss层。

代码

class NumpyMLP:
    def __init__(self, input_size=784, hidden_size=128, num_classes=10):
        self.linear1 = NumpyLinear(input_size, hidden_size)
        self.relu1 = NumpyReLU()
        self.linear2 = NumpyLinear(hidden_size, hidden_size)
        self.relu2 = NumpyReLU()
        self.linear3 = NumpyLinear(hidden_size, num_classes)
        self.softmax = NumpySoftmax()
        self.update_layers = [self.linear1, self.linear2, self.linear3]
        
    def forward(self, x):
        x = self.linear1(x)
        x = self.relu1(x)
        x = self.linear2(x)
        x = self.relu2(x)
        x = self.linear3(x)
        x = self.softmax(x)
        return x
    
    def get_loss(self, labels):
        return self.softmax.get_loss(labels)
    
    def backward(self):
        grad = self.softmax.backward()
        grad = self.linear3.backward(grad)
        grad = self.relu2.backward(grad)
        grad = self.linear2.backward(grad)
        grad = self.relu1.backward(grad)
        grad = self.linear1.backward(grad)
        
    def update_params(self, lr=0.01):
        for layer in self.update_layers:
            layer.update_params(lr)
    
    def __call__(self, x):
        return self.forward(x)

六、模型训练

训练过程描述

在一个 mini-batch 随机梯度下降 (SGD) 训练过程中，我们会逐步执行以下步骤来训练模型：

前向传播：对于每个 mini-batch 数据，我们将输入 x 传入 forward 方法。模型按层顺序计算线性变换、ReLU 激活和 softmax 预测概率。
计算损失：前向传播得到的预测输出将与实际标签 labels 一起传入 get_loss 方法，计算交叉熵损失。
反向传播：损失计算完成后，通过调用 backward 方法，模型按层逆序逐步传播梯度。softmax 层的 backward 返回初始梯度，后续每层根据前一层传入的梯度进行自身的反向传播计算，并传递给下一层。
参数更新：反向传播完成后，调用 update_params 方法，按学习率 lr 更新各层权重和偏置。该更新通过遍历 update_layers 中的可训练层（例如每个 NumpyLinear 层）逐步完成。
重复迭代：完成一个 mini-batch 的训练后，data_loader从下一个 mini-batch 获取新的训练样本，重复上述步骤，直到所有 mini-batch 均参与训练。在一个训练集训练完毕后，还需执行多个 epoch。

一次完整训练

为了减少超参，将隐藏层的大小都设置为hidden_size$\times$hidden_size维，于是我们有四个超参

hidden_size
batch_size
num_epochs // 训练集
lr // 学习率

对于一个超参组合，一次完整训练过程如下所示：

hidden_size = 128
batch_size = 32
num_epochs = 10
lr = 0.01

train_loader = NumpyDataLoader(img_train_np, label_train_np, batch_size=batch_size, shuffle=True)
test_loader = NumpyDataLoader(img_test_np, label_test_np, batch_size=batch_size, shuffle=False)

model = NumpyMLP(hidden_size=hidden_size)
init_params = model.export_parameters()

print('Training Numpy model...')
for epoch in range(num_epochs):
    running_loss = 0.0
    for images, labels in train_loader:
        y_pred = model(images)
        running_loss += model.get_loss(labels)
        model.backward()
        model.update_params(lr=lr)

    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {running_loss/len(train_loader):.4f}')

寻找最优超参

num_epochs 和lr直接影响一次训练的程度，不好直接比较优劣，因此我们讨论hidden_size和batch_size对模型的影响，通过验证集来评估。

# 参数设置
hidden_sizes = [32, 64, 128, 256]
batch_sizes = [8, 16, 32, 64]
learning_rate = 0.01
num_epochs = 10

# 用于保存验证集准确率的矩阵
accuracy_matrix = np.zeros((len(hidden_sizes), len(batch_sizes)))

best_accuracy = 0
best_params = {}

# 超参数搜索
for i, hidden_size in enumerate(hidden_sizes):
    for j, batch_size in enumerate(batch_sizes):
        # 初始化数据加载器和模型
        train_loader = NumpyDataLoader(img_train_np, label_train_np, batch_size=batch_size, shuffle=True)
        val_loader = NumpyDataLoader(img_val_np, label_val_np, batch_size=batch_size, shuffle=False)
        model = NumpyMLP(hidden_size=hidden_size)

        # 训练模型
        for epoch in range(num_epochs):
            for images, labels in train_loader:
                y_pred = model(images)
                model.get_loss(labels)
                model.backward()
                model.update_params(lr=learning_rate)

        # 计算验证集准确率
        correct = 0
        total = 0
        for images, labels in val_loader:
            y_pred = model(images)
            predicted = np.argmax(y_pred, axis=1)
            total += labels.size
            correct += (predicted == labels).sum()

        accuracy = 100 * correct / total
        accuracy_matrix[i, j] = accuracy  # 保存准确率到矩阵中

        # 打印并更新最佳参数
        print(f'Params: hidden_size={hidden_size}, batch_size={batch_size} | Validation Accuracy: {accuracy:.2f}%')
        if accuracy > best_accuracy:
            best_accuracy = accuracy
            best_params = {
                'hidden_size': hidden_size,
                'batch_size': batch_size,
            }

print(f'Best params: {best_params} with accuracy: {best_accuracy:.2f}%')

可视化结果

将得到的最优超参训练的模型用于测试集，结果如下，热力图的幅值表示该超参组合的模型在验证集上的准确率。

loss

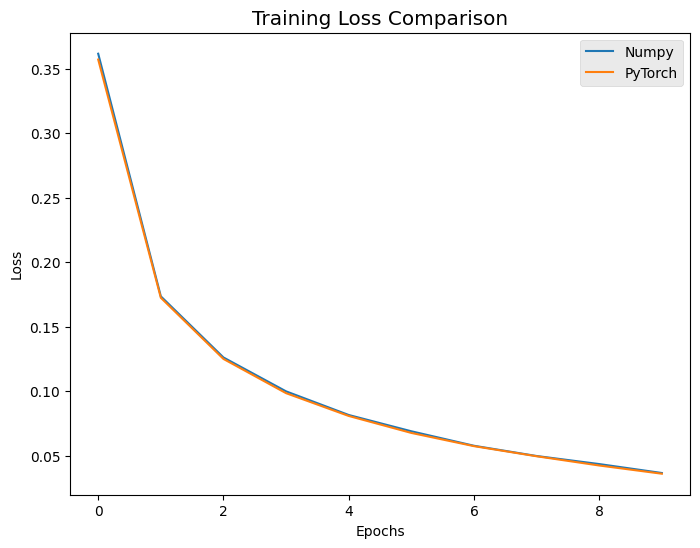
大体趋势为Batch_size越小，Hidden_size越大，效果越好，但也需要更多训练时间和更多epochs数，如左下角 (8, 256) 组合略逊于上方 (8, 128) 组合，可能是因为训练不够充分所致。

最终，我们采用 (8, 128) 组合最为 (Batch_size, Hidden_size) 超参组合。

七、模型评估

用Pytorch重写一份相同的MLP模型，在相同的超参数设置下进行训练，并且网络初始化参数也保持一致，结果如下：

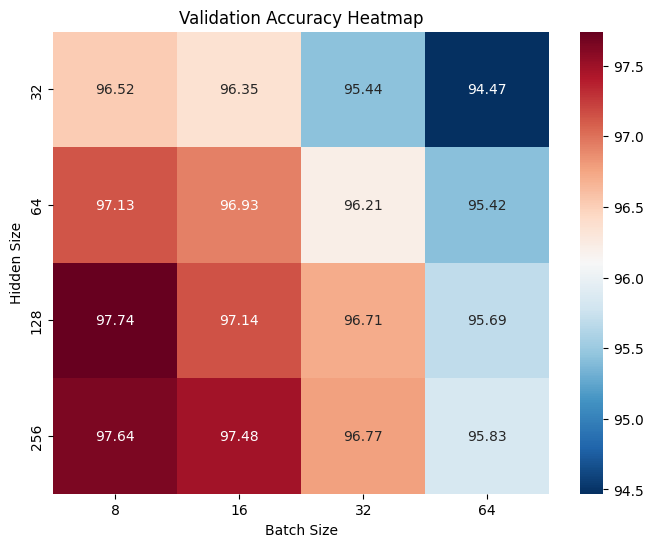
train

可以看出，训练过程相差无几，证明了我们手动构建的模型与Pytorch的一致性，同时两者在测试集上的准确度如下：

Numpy：97.68%
Pytorch：97.61%

结果也非常接近。

使用Numpy实现全连接神经网络

一、数据集的下载和处理

下载数据

数据处理与分割

数据集加载器

二、全连接层

全连接层->向前传播

全连接层->反向传播

全连接层->参数初始化

全连接层->参数更新

三、ReLU激活层

ReLU层->前向传播

ReLU层->反向传播

四、Softmax-Loss层

Softmax层->前向传播

Loss层->前向传播

Softmax-Loss层->反向传播

五、搭建全连接神经网络

六、模型训练

训练过程描述

一次完整训练

寻找最优超参

七、模型评估